Principe de l'énergie libre

Le principe d'énergie libre est un cadre utilisé pour décrire comment le cerveau prend des décisions et s'adapte à des circonstances changeantes. Il repose sur l'idée que le cerveau essaie constamment de minimiser son énergie libre, qui est une mesure de la surprise que le cerveau ressent face aux informations sensorielles qu'il reçoit.

En minimisant son énergie libre, le cerveau peut faire des prédictions sur le monde qui l'entoure et prendre les actions appropriées. La minimisation implicite de l'énergie libre variationnelle est formellement liée aux méthodes bayésiennes variationnelles et a été introduite à l'origine par Karl Friston comme explication de la perception incarnée dans les neurosciences, où elle est aussi connue sous le nom d'inférence active ou de codage prédictif.

En termes généraux, le principe de l'énergie libre est utilisé pour décrire un système tel que défini comme étant enfermé dans une couverture de Markov - essaie de minimiser la différence entre son modèle du monde et la perception de ses capteurs. Cette différence peut être qualifiée de « surprise » et minimisée par une mise à jour constante du modèle du monde. En tant que tel, le principe est basé sur l'idée bayésienne du cerveau comme « moteur d'inférence ». Friston a ajouté une deuxième voie à la minimisation : l'action. En changeant activement le monde dans l'état attendu, les systèmes peuvent aussi minimiser l'énergie libre du système. Friston suppose que c'est le principe de toute réaction biologique.

Friston considère que son principe s'applique aussi bien aux troubles mentaux qu'à l'intelligence artificielle. Les implémentations de l'IA basées sur le principe de l'inférence active ont montré des avantages par rapport à d'autres méthodes. Il est également utilisé pour expliquer comment les systèmes biologiques se maintiennent en état de non-équilibre quasi-stationnaire en se limitant à un nombre limité d'états

Définitions

Codage prédictif

Le codage prédictif est une théorie de neurosciences sur la manière dont le cerveau traite les informations sensorielles. Elle propose que le cerveau génère constamment des prévisions sur les entrées sensorielles qu'il est susceptible de recevoir, en fonction de son expérience passée et de son contexte actuel. Lorsque de nouvelles entrées sensorielles sont reçues, elles sont comparées à ces prévisions, et toutes les différences sont utilisées pour mettre à jour le modèle interne du cerveau à propos du monde. Ce processus permet au cerveau de traiter rapidement et efficacement les informations sensorielles, ce qui nous permet d'interagir avec notre environnement en temps réel.

Inférence active

L'inférence active est le cadre computationnel qui décrit comment un agent (comme une personne ou une intelligence artificielle) peut interagir avec son environnement pour atteindre un résultat souhaité. Il repose sur l'idée qu'un agent peut maximiser ses chances de réussite en recherchant activement des informations sur son environnement et en utilisant ces informations pour faire des prévisions sur les événements futurs. Ces prévisions peuvent alors être utilisées pour orienter les actions de l'agent de manière cohérente avec ses objectifs et ses préférences.

Energie libre

L'énergie libre est une mesure de l'incertitude ou de la surprise dans un système. Elle est définie comme la différence entre l'énergie attendue du système et l'énergie réelle du système.

Dans la théorie de Karl Friston, le but d'un système intelligent, tel que le cerveau, est de minimiser son énergie libre en réduisant l'incertitude et la surprise. Cela est réalisé en faisant des prédictions sur l'état futur du système, puis en utilisant les informations sensorielles pour mettre à jour ces prédictions et réduire l'erreur ou la discordance entre les états prédits et réels.

En d'autres termes est une mesure de l'écart ou de l'erreur entre les prédictions du système et les entrées sensorielles réelles qu'il reçoit. En minimisant son énergie libre le système peut réduire l'incertitude et la surprise, et s'adapter à son environnement de manière plus efficace.

Formalisme

Formulation continue

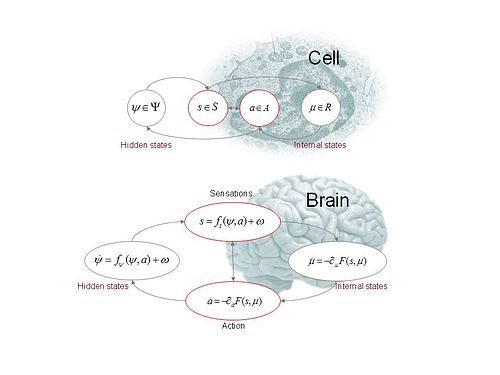
L'inférence active repose sur le tuple ${\displaystyle (\Omega ,\Psi ,S,A,R,q,p)}$,

• Un échantillon de l'espace ${\displaystyle \Omega }$ – à partir de laquelle les fluctuations aléatoires ${\displaystyle \omega \in \Omega }$ sont tirées
• États cachés ou externes ${\displaystyle \Psi :\Psi \times A\times \Omega \to \mathbb {R} }$ – qui provoquent des états sensoriels et dépendent de l'action
• États sensoriels ${\displaystyle S:\Psi \times A\times \Omega \to \mathbb {R} }$ – une cartographie probabiliste à partir de l'action et des états cachés
• Action ${\displaystyle A:S\times R\to \mathbb {R} }$ – qui dépend des états sensoriels et internes
• États internes ${\displaystyle R:R\times S\to \mathbb {R} }$ – qui provoquent l'action et dépendent des états sensoriels
• Densité générative ${\displaystyle p(s,\psi |m)}$ – sur des états sensoriels et cachés sous un modèle génératif ${\displaystyle m}$
• Densité variationnelle ${\displaystyle q(\psi |\mu )}$ – sur des états cachés ${\displaystyle \psi \in \Psi }$ paramétrée par des états internes ${\displaystyle \mu \in R}$

Action et perception

L'objectif est de maximiser la preuve du modèle ${\displaystyle p(s|m)}$ ou de minimiser la surprise ${\displaystyle -\log p(s|m)}$. Il s'agit généralement d'une marginalisation insoluble sur les états cachés, donc la surprise est remplacée par une énergie libre variationnelle supérieure liée. Cependant, cela signifie que les états internes doivent également minimiser l'énergie libre, car l'énergie libre est une fonction des états sensoriels et internes :

${\displaystyle a(t)={\underset {a}{\operatorname {arg\,min} }}\{F(s(t),\mu (t))\}}$

${\displaystyle \mu (t)={\underset {\mu }{\operatorname {arg\,min} }}\{F(s(t),\mu ))\}}$

${\displaystyle {\underset {\mathrm {energie-libre} }{\underbrace {F(s,\mu )} }}={\underset {\mathrm {energie} }{\underbrace {E_{q}[-\log p(s,\psi \mid m)]} }}-{\underset {\mathrm {entropie} }{\underbrace {H[q(\psi |\mu )]} }}={\underset {\mathrm {surprise} }{\underbrace {-\log p(s|m)} }}+{\underset {\mathrm {divergence} }{\underbrace {D_{\mathrm {KL} }[q(\psi |\mu )\|p(\psi \mid s,m)]} }}\geq {\underset {\mathrm {surprise} }{\underbrace {-\log p(s|m)} }}}$

Ceci induit une double minimisation par rapport à l'action et aux états internes qui correspondent respectivement à l'action et à la perception.

Comparaison avec d'autres cadres

L'idée que les systèmes biologiques auto-organisés - comme une cellule ou un cerveau - peuvent être compris comme minimisant l'énergie libre variationnelle est basée sur les observations de Helmholtz sur l'inférence inconsciente et les traitements ultérieurs en psychologie et en apprentissage automatique.

L'énergie libre variationnelle est fonction de certains résultats et d'une densité de probabilité sur leurs causes (cachées). Cette densité variationnelle est définie par rapport à un modèle probabiliste qui génère des résultats à partir des causes. Dans ce contexte, l'énergie libre fournit une approximation (limite supérieure) des données probantes du modèle bayésien. Sa minimisation peut donc être utilisée pour expliquer l'inférence et l'apprentissage bayésiens. Lorsqu'un système échantillonne activement les résultats pour minimiser l'énergie libre, il effectue implicitement une inférence active et maximise les preuves pour son modèle (génératif).

Entropie

Cependant, l'énergie libre est aussi une limite supérieure sur l'auto-information (ou surprise) des résultats, où la moyenne à long terme de la surprise est l'entropie. Cela signifie que si un système agit pour minimiser l'énergie libre, il placera implicitement une limite supérieure sur l'entropie des résultats - ou états sensoriels - qu'il échantillonne.

Minimisation de l'énergie libre et auto-organisation

La minimisation de l'énergie libre a été proposée comme caractéristique des systèmes auto-organisés, lorsqu'elle est présentée comme des systèmes dynamiques aléatoires. Cette formulation repose sur une couverture de Markov (comprenant des états d'action et des états sensoriels) qui sépare les états internes et externes. Si les états internes et l'action minimisent l'énergie libre, alors ils placent une limite supérieure sur l'entropie des états sensoriels

${\displaystyle \lim _{T\to \infty }{\frac {1}{T}}{\underset {\mathrm {free-action} }{\underbrace {\int _{0}^{T}F(s(t),\mu (t))dt} }}\geq \lim _{T\to \infty }{\frac {1}{T}}\int _{0}^{T}{\underset {\mathrm {surprise} }{\underbrace {-\log p(s(t)|m)} }}dt=H[p(s|m)]}$

En effet, dans les hypothèses ergodiques, la moyenne à long terme des surprises est l'entropie. Cette limite résiste à une tendance naturelle au désordre - du type associé à la deuxième loi de la thermodynamique et au théorème de fluctuation.

Minimisation de l'énergie libre et inférence bayésienne

Toutes les inférences bayésiennes peuvent être exprimées en termes de minimisation de l'énergie libre, par exemple lorsque l'énergie libre est minimisée par rapport aux états internes, la divergence de Kullback-Leibler entre la densité variationnelle et la densité postérieure sur les états cachés est minimisée. Cela correspond à une inférence bayésienne approximative - lorsque la forme de la densité variationnelle est fixe - et à une inférence bayésienne exacte sinon. La minimisation de l'énergie libre fournit donc une description générique de l'inférence et du filtrage bayésiens (p. ex. filtre de Kalman). Elle est également utilisée dans la sélection de modèles bayésiens, où l'énergie libre peut être utilement décomposée en complexité et précision :

${\displaystyle {\underset {\mathrm {energie-libre} }{\underbrace {F(s,\mu )} }}={\underset {\mathrm {complexite} }{\underbrace {D_{\mathrm {KL} }[q(\psi |\mu )\|p(\psi |m)]} }}-{\underset {\mathrm {precision} }{\underbrace {E_{q}[\log p(s|\psi ,m)]} }}}$

Les modèles avec un minimum d'énergie libre fournissent une explication précise des données, sous les coûts de complexité (c.f., le rasoir d'Ockham et les traitements plus formels des coûts de calcul)). Ici, la complexité est la divergence entre la densité variationnelle et les croyances antérieures sur les états cachés (c'est-à-dire les degrés effectifs de liberté utilisés pour expliquer les données).

Minimisation de l'énergie libre et thermodynamique

L'énergie libre variationnelle est une information théorique fonctionnelle et se distingue de l'énergie libre thermodynamique (Helmholtz). Cependant, le terme de complexité de l'énergie libre variationnelle partage le même point fixe que l'énergie libre de Helmholtz (dans l'hypothèse où le système est fermé thermodynamiquement mais non isolé). En effet, si les perturbations sensorielles sont suspendues (pour une période de temps suffisamment longue), la complexité est minimisée (car la précision peut être négligée). À ce stade, le système est en équilibre et les états internes minimisent l'énergie libre de Helmholtz, par le principe de l'énergie minimale.

Minimisation de l'énergie libre et théorie de l'information

La minimisation de l'énergie libre équivaut à maximiser l'information mutuelle entre les états sensoriels et les états internes qui paramètrent la densité variationnelle (pour une densité variationnelle à entropie fixe). Ceci relie la minimisation de l'énergie libre au principe de la redondance minimale et aux traitements connexes utilisant la théorie de l'information pour décrire le comportement optimal.

Dans d'autres domaines

L'inférence active est étroitement liée au théorème du bon régulateur et aux comptes-rendus connexes de l'auto-organisation, tels que l'auto-assemblage, la formation de motifs, l'autopoïèse et la practopoièse. Elle aborde les thèmes de la cybernétique, la synergétique et l'embodiment. Puisque l'énergie libre peut être exprimée comme l'énergie attendue (des résultats) sous la densité variationnelle moins son entropie, elle est également liée au principe d'entropie maximale. Enfin, parce que la moyenne temporelle de l'énergie est l'action, le principe de l'énergie libre variationnelle minimale est un principe de moindre action.

En neurosciences computationelles

La minimisation de l'énergie libre fournit un moyen utile de formuler des modèles normatifs (optimaux de Bayes) d'inférence neuronale et d'apprentissage sous incertitude et souscrit donc à l'hypothèse bayésienne du cerveau. Les processus neuronaux décrits par la minimisation de l'énergie libre dépendent de la nature des états cachés : ${\displaystyle \Psi =X\times \Theta \times \Pi }$ qui peuvent comprendre des variables dépendantes du temps, des paramètres invariants dans le temps et la précision (variance inverse ou température) des fluctuations aléatoires. La minimisation des variables, des paramètres et de la précision correspond respectivement à l'inférence, à l'apprentissage et au codage de l'incertitude.

Inférence perceptuelle et catégorisation

La minimisation de l'énergie libre formalise la notion d'inférence inconsciente dans la perception et fournit une théorie normative (bayésienne) du traitement neuronal. La théorie des processus associés de la dynamique neuronale est basée sur la minimisation de l'énergie libre par la descente de gradient. Ceci correspond au filtrage bayésien généralisé (où ~ désigne une variable en coordonnées de mouvement généralisées et ${\displaystyle D}$ est un opérateur de matrice dérivée) :

${\displaystyle {\dot {\tilde {\mu }}}=D{\tilde {\mu }}-\partial _{\tilde {\mu }}F(s,{\tilde {\mu }})}$

Habituellement, les modèles génératifs qui définissent l'énergie libre sont non linéaires et hiérarchiques (comme les hiérarchies corticales dans le cerveau). Parmi les cas particuliers de filtrage généralisé, on peut citer le filtrage de Kalman, qui est formellement équivalent au codage prédictif – une métaphore populaire pour le message qui passe dans le cerveau. Dans les modèles hiérarchiques, le codage prédictif implique l'échange récurrent d'erreurs de prédiction ascendantes (bottom-up) et descendantes (top-down) qui est compatible avec l'anatomie et la physiologie des systèmes sensoriel et moteur.

Apprentissage perceptif et mémoire

Dans le codage prédictif, l'optimisation des paramètres du modèle par une montée en gradient sur l'intégrale temporelle de l'énergie libre (action libre) se réduit à une plasticité associative ou Hebbienne et est associée à une plasticité synaptique dans le cerveau.

Précision perceptuelle, attention et prépondérance

L'optimisation des paramètres de précision correspond à l'optimisation du gain des erreurs de prédiction (c.f. gain de Kalman). Dans les implémentations neuronalement plausibles du codage prédictif, cela correspond à l'optimisation de l'excitabilité des cellules pyramidales superficielles et a été interprété en termes de gain attentionnel.

En psychiatrie

L'inférence active a été utilisée pour aborder un éventail de questions en neuropsychiatrie, notamment l'observation de l'action, les neurones miroirs, les saccades et la recherche visuelle, les mouvements oculaires, le sommeil, les illusions, l'attention, la sélection des actions, l'hystérie et la psychose

Inférence active et théorie (des jeux) de la décision optimale

Les problèmes de décision optimale (habituellement formulés comme des processus de décision de Markov partiellement observables) sont traités par inférence active en absorbant les fonctions d'utilité dans des croyances antérieures. Dans ce paramètre, les états qui ont une utilité élevée (faible coût) sont les états qu'un agent s'attend à occuper. En équipant le modèle générateur d'états cachés qui contrôlent le modèle, les politiques (séquences de contrôle) qui minimisent l'énergie libre variationnelle conduisent à des états d'utilité élevée.

Neurobiologiquement, les neuromodulateurs comme la dopamine sont considérés pour rapporter la précision des erreurs de prédiction en modulant le gain des cellules principales codant l'erreur de prédiction. Cela est étroitement lié au rôle de la dopamine dans la déclaration des erreurs de prévision en soi, mais en est formellement distinct et dans les comptes rendus informatiques connexes.

Mathématiques

Lorsque la descente de gradient est appliquée à l'action ${\displaystyle {\dot {a}}=-\partial _{a}F(s,{\tilde {\mu }})}$ le contrôle moteur peut être compris en termes d'arcs réflexes classiques qui sont engagés par des prédictions descendantes (corticospinales). Ceci fournit un formalisme qui généralise la solution du point d'équilibre - au problème des degrés de liberté - aux trajectoires de mouvement.

Inférence et contrôle optimal

L'inférence active est liée au contrôle optimal en remplaçant les fonctions de valeur ou de coût à emporter par des croyances préalables sur les transitions d'état ou le débit. Ceci exploite le lien étroit entre le filtrage bayésien et la solution à l'équation de Bellman. Cependant, l'inférence active commence par (prend le pas sur) le débit ${\displaystyle f=\Gamma \cdot \nabla V+\nabla \times W}$ qui sont spécifiés par des fonctions de valeur scalaire ${\displaystyle V(x)}$ et vectorielle ${\displaystyle W(x)}$ de l'espace d'état (c.f. la décomposition de Helmholtz). Ici, ${\displaystyle \Gamma }$ est l'amplitude des fluctuations aléatoires et le coût est ${\displaystyle c(x)=f\cdot \nabla V+\nabla \cdot \Gamma \cdot V}$. Les antécédents de dépassement du flux ${\displaystyle p({\tilde {x}}|m)}$ induisent une priorité sur les états ${\displaystyle p(x|m)=\exp(V(x))}$ qui est la solution aux équations de Kolmogorov avancées appropriées. En revanche, la régulation optimale optimise le débit, compte tenu d'une fonction de coût, en supposant que ${\displaystyle W=0}$ (c'est-à-dire que le débit n'est pas bouclé ou qu'il présente un bilan détaillé). Habituellement, il s'agit de résoudre les équations de Kolmogorov rétrogrades

Références

Voir aussi

Articles connexes

• Affordance
• Autopoïèse
• Théorie de la décision
• Embodiment
• Énergie libre
• Commande optimale
• Auto-organisation

Liens externes

• Sciences du comportement et du cerveau (Andy Clark)

• Portail de l’énergie
• Portail de la biologie
• Portail des neurosciences