Algorithme de Smith-Waterman
L'algorithme de Smith-Waterman est un algorithme d'alignement de séquences utilisé notamment en bioinformatique. Il a été inventé par Temple F. Smith (en) et Michael S. Waterman en 1981.
L'algorithme de Smith-Waterman est un algorithme optimal qui donne un alignement correspondant au meilleur score possible de correspondance entre les acides aminés ou les nucléotides des deux séquences. Le calcul de ce score repose sur l'utilisation de matrices de similarité ou matrices de substitution.
L'algorithme est par exemple utilisé pour aligner des séquences de nucléotides ou de protéines, notamment pour la prédiction de gènes, la phylogénie ou la prédiction de fonction.
Alignement et score
L'algorithme de Smith et Waterman cherche à optimiser l'alignement de deux séquences biologiques qui sont traitées comme des chaînes de caractères. Pour réaliser cet alignement, on peut insérer des "trous" ou indel (symbolisés par des tirets dans l'exemple ci-dessous) dans l'une ou l'autre séquence, afin de maximiser le nombre de coïncidences de caractères entre les deux séquences. Il existe théoriquement un grand nombre possible de manières d'aligner deux séquences, ainsi que le montre l'exemple ci-dessous :
FATCA-TY FATCATY FATCATY---
|| | | || |: |||:
CATFAST- CATFAST ---CATFAST
S'agissant des séquences protéiques, il faut de plus tenir compte non seulement des conservations strictes d'acides aminés (symbolisées par des tirets verticaux dans l'exemple ci-dessus), mais aussi des remplacements conservatifs, où un acide aminé est remplacé par un acide aminé proche sur le plan physico-chimique (symbolisés par des "deux-points" dans l'exemple ci-dessus). Pour tenir compte de cela, on utilise des fonctions de score qui permettent de quantifier le résultat du remplacement de l'acide aminé a par l'acide aminé b. Ces fonctions de score sont représentées sous forme de matrices appelées matrices de similarité. Le score de l'alignement de a avec b est donné par le coefficient D(a, b) de la matrice de similarité.
Ces matrices de similarité sont complétées par une pénalité associée aux indels (insertions ou délétions) : D(a, -) = D(-, a) = Δ. Ce score Δ est négatif, pour pénaliser l'introduction d'insertions dans l'alignement. Le score d'un alignement de séquences donné est calculé à partir de la somme des scores des alignements individuels des caractères (acides aminés ou trous). L'algorithme de Smith-Waterman permet de trouver un alignement qui réalise le score optimal.
Principe et comparaison avec les autres algorithmes
Comme l'algorithme de Needleman-Wunsch auquel il est apparenté, il utilise la programmation dynamique. Contrairement à l'algorithme BLAST (Basic Local Alignment Search Tool) plus rapide, l'algorithme de Smith-Waterman garantit l'optimalité de la solution. La différence avec l'algorithme de Needleman-Wunsch est qu'alors que ce dernier recherche des alignements de séquence globaux (impliquant toute la longueur des deux séquences à aligner), l'algorithme de Smith-Waterman recherche aussi des alignements locaux, n'impliquant que des régions ou segments des deux séquences analysées. Il permet donc par exemple de repérer des protéines qui possèdent un domaine en commun parmi d'autres domaines différents.
Comme toutes les méthodes reposant sur la programmation dynamique, l'algorithme Smith-Waterman construit la solution du problème complet sur celles de problèmes de taille plus petite. Par exemple, si on doit aligner deux séquences A et B de longueurs respectives l et n, la méthode consiste à s'appuyer sur les alignements des séquences de longueurs plus courtes. La méthode de Smith et Waterman détermine ainsi tous les meilleurs scores possibles pour les alignements des i premiers acides aminés (ou nucléotides) de A et des j premiers acides aminés (ou nucléotides) de B, pour toutes les valeurs 1 ≤ i ≤ l et toutes les valeurs 1 ≤ j ≤ n. On construit progressivement ainsi une table l x n des scores de tous les sous-alignements possibles. L'analyse de la table permet ensuite de trouver un alignement donnant le score optimal.
L'algorithme
La recherche de l'alignement optimal entre deux séquences A et B de longueurs respectives l et n se fait en deux phases distinctes :
- Le calcul de la matrice M des scores d'alignement partiel. C'est une matrice l x n, dont chaque coefficient M(i, j) donne le score de l'alignement des i premiers acides aminés (ou nucléotides) de A avec les j premiers acides aminés de B. Ce calcul se fait itérativement, à partir des scores des alignements partiels plus courts. Une fois la matrice remplie, le coefficient du coin inférieur droit de la matrice, M(l, n), donne le score de l'alignement optimal complet entre A et B.
- La construction de l'alignement à partir de la matrice M. En partant du coin inférieur droit, on remonte dans la matrice pour déterminer par quel chemin on a obtenu le score optimal. Ce chemin correspond à l'alignement optimal.
Ces deux phases sont décrites ci-dessous.
Calcul de la matrice des scores
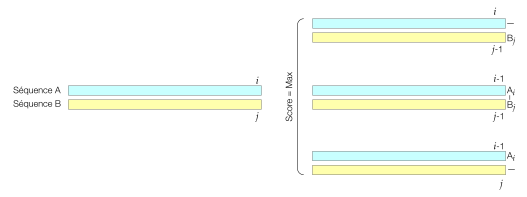
Le principe de la construction de la matrice M(i, j) est décrit sur le schéma ci-dessous :
Le coefficient M(i, j) de la matrice correspond au score du meilleur alignement des i premiers acides aminés (ou nucléotides) de la séquence A avec les j premiers de B. On peut distinguer trois cas possibles :
- Soit le meilleur alignement se termine par la correspondance de Ai avec Bj (cas du milieu sur le schéma ci-dessus). Dans ce cas, on a M(i, j)=M(i-1, j-1)+D(Ai, Bj).
- Soit le meilleur alignement se termine par la correspondance de Bj avec un trou dans la séquence A (cas du haut sur le schéma ci-dessus). Dans ce cas on a M(i, j)=M(i, j-1)+Δ
- Soit le meilleur alignement se termine par la correspondance de Ai avec un trou dans la séquence B (cas du bas sur le schéma ci-dessus). Dans ce cas on a M(i, j)=M(i-1, j)+Δ
Avec D(Ai, Bj) le score d'alignement de l'acide aminé i de A avec l'acide aminé j de B, tiré de la matrice de similarité, et Δ, la pénalité associée à un indel.
On peut résumer la méthode de calcul de la matrice M comme suit :

Lorsqu'il n'y a pas de régions similaires entre les deux séquences A et B, les scores obtenus sont négatifs (absence de coïncidences). Le fait de rajouter la valeur zéro comme premier terme de l'alternative permet à l'algorithme de Smith et Waterman de repérer des alignements locaux.
Construction de l'alignement
Une fois la matrice M construite, on recherche les maximums locaux dans la matrice, supérieurs à une valeur seuil, fixée par l'utilisateur. Ces maximums correspondent aux positions de fins d'alignement : Si M(x, y) est un tel maximum, cela signifie qu'il existe un alignement optimum local qui se termine par l'alignement de Ax avec By.
Pour déterminer cet alignement, il faut alors remonter dans la matrice M pour déterminer par quel chemin on est arrivé à ce score, c'est-à-dire par quelle option de l'alternative ci-dessus on a obtenu la valeur du coefficient de la matrice. Pour chaque i, j lors de la remontée :
- si on a M(i, j)=M(i-1,j-1)+D(Ai, Bj), alors on aligne Ai avec Bj et on remonte à M(i-1,j-1) ;
- si on a M(i, j)=M(i, j-1)+Δ, alors on aligne Bj avec un trou et on remonte à M(i, j-1) ;
- si on a M(i, j)=M(i-1, j)+Δ, alors on aligne Ai avec un trou et on remonte à M(i-1, j) ;
- si on a M(i, j)=0, l'alignement local est terminé.
On effectue cette remontée à partir de tous les maximums locaux M(x, y) pour obtenir tous les alignements locaux optimaux
Exemple
Le schéma ci-dessous montre l'application de l'algorithme de Smith-Waterman à deux courtes séquences protéiques : FATCATY et TCAGSFA.

La matrice M(i, j) est remplie de gauche à droite et de haut en bas à l'aide du principe de récurrence décrit plus haut. Une fois le calcul terminé, on recherche le coefficient le plus élevé (score maximum). À partir de ce coefficient, on retrace le chemin par lequel ce score a été obtenu, ce qui permet de déduire l'alignement de score optimal, indiqué à droite. Cet alignement comporte trois conservations strictes, un indel, et deux remplacements conservatifs (acide aminé remplacé par un acide aminé similaire, mais non identique). Ces derniers sont indiqués par un caractère "deux points".
Améliorations
Une version améliorée de l'algorithme de Smtih-Waterman a été proposée par Osamu Gotoh. Cette amélioration consiste à introduire une fonction de coût affine pour les trous en fonction de leur longueur. Dans l'algorithme standard de Smith-Waterman, le coût d'un trou de longueur k est k.Δ, soit un coût linéaire en fonction de la longueur. Dans l'algorithme de Gotoh, ce coût est affine, de la forme α + k.β, avec α > β. Ceci permet de favoriser le regroupement des indels et d'éviter la multiplication de petits trous, ce qui est conforme à ce qui se passe au niveau biologique, où les insertions et délétions sont regroupées au niveau des boucles de surface de la structure de la protéine correspondante.